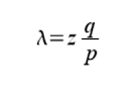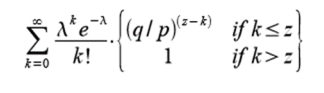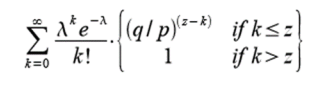ビットコイン： P2P 電子通貨システム
概要
完全なP2P電子通貨の実現により、金融機関の介在無しに、利用者同士の直接的なオンライン決済が可能となるだろう。電子署名により、P2P電子通貨の機能の一部は実現可能であるが、その機能の主な利点は、信用が置ける第三者機関が二重支払いを防ぐために必要とされる場合、失われることとなる。本論文では、P2Pネットワークの使用による、二重支払い問題の解決策を提案する。
このネットワークでは各トランザクションを、ハッシュ関数に基づいたProof-of-workの進行中のブロックチェーン上にハッシュ化することで、タイムスタンプを行う。これにより、Proof-of-workの計算を再度行わなければ変更不可能な記録を生成するのである。
最長のブロックチェーンは、一連のトランザクション履歴を証明するだけでなく、それが最大のCPUパワーを保有するプールから生成されたものであることを証明する。善意のノードが過半数のCPUパワーをコントロールする限り、最長のチェーンを生成し続け、攻撃者を退けることが可能である。ネットワーク自体は必要最小限の構成で良い。
メッセージはベストエフォート方式でブロードキャストすれば良く、各ノードはネットワークにいつ離脱・再接続しても問題ない。これは、各ノードが再接続時に最長のブロックチェーンを受け入れることで、離脱している間に何が生じたか把握することができるためである。
序論
現在のインターネット上の商取引は殆ど例外なく、電子取引を処理する信用の置ける第三者の金融機関に依存している。大多数の取引はこの仕組みで問題なく執り行われるが、信頼に基づくモデルであるが故の脆弱性が問題となる。つまり、金融機関には争議仲裁という避けられない責任があるため、完全に不可逆的な取引の提供はできないのである。仲裁コストに伴う取引コストの増加により、取引規模が限定される結果、小額取引が不可能となる。
また、不可逆的サービスに対する不可逆的支払ができない事によるコストは更に多大となる。可逆的取引には一層の信用が必要であるため、販売者は購入者に対して用心深くならざるを得ず、購入者に必要以上に多くの情報を求めるのである。また、一定割合の詐欺は避けられないものとして受け入れられている。これらのコストや支払いの不確実性は、物理的な通貨を使用すれば避けることが可能だが、電子取引では信用の置ける第三者を介さずに支払いを可能とするようなメカニズムは存在しない。
必要なのは信用ではなく、暗号学的証明に基づいた電子取引システムであり、これにより信用の置ける第三者を介さずに、利用者間の直接取引が可能となる。計算理論上不可逆な取引は、売り手を詐欺から守り、また、買い手を保護するためのエスクロー（第三者預託）機能は容易に実装可能である。本論文では、取引が時系列に行われたかについて、計算に基づいた証明を生成するP2P分散型タイムスタンプサーバを使用し、二重支払い問題の解決策を提案する。本システムは、善意のノードが攻撃者グループのノードを上回るCPUパワーをコントロールしている限り安全である。
トランザクション
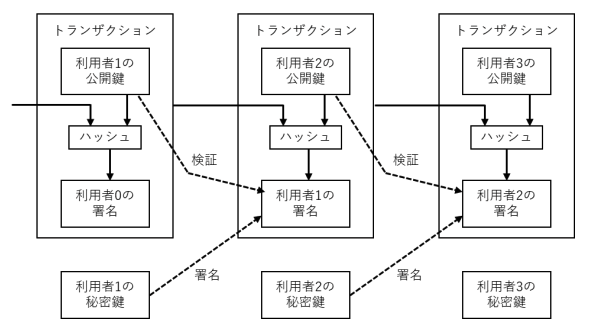
本論文では、コインをチェーンのように連続した電子署名と定義する。各コインの所有者は、自分のトランザクションと次の所有者の公開鍵をハッシュ化したものに電子署名を行い、これらを電子通貨の末尾に加えることによって、次の所有者にコインを転送する。受取人は一連の電子署名を検証することで、過去の所有権を確認できる。
問題点は、受取人はコインの所有者が過去に二重支払いをしたか否かの検証ができない事である。一般的な解決策としては、信用の置ける中央機関または造幣局を仲介させ、二重支払いの有無につき全トランザクションを確認させる事である。つまり、トランザクション成立毎にコインが造幣局に返却されて新たなコインが発行され、造幣局が直接発行したコインであることが、二重支払いが行われてない事の信用となる。この解決策では、全トランザクションが造幣局経由で行われるため、銀行と同様、造幣局の運営組織に金融システムの運命が左右される問題がある。
必要なのは、コインの受取人に、過去の所有者達が過去のトランザクションに署名していない事を知らせる方法である。この目的では、最初のトランザクションのみをカウントし、後の二重支払いの試みはカウントしない。トランザクションが無かった事を明確にする唯一の方法は、全トランザクションを監視する事である。造幣局モデルでは、造幣局が全トランザクションを監視して最初のトランザクションがどれかを決定していた。これを信用の置ける第三者機関を介さず行うには、トランザクションが公開され[1]、参加者達が受け取った順番通りのトランザクション履歴に合意できるシステムが必要となる。受取人は各トランザクション時点において、大多数のノードが各コインが初めて受け取られた事を同意した、という証明を必要とする。
タイムスタンプサーバ
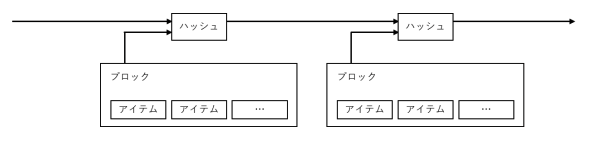
本論文で提案する解決策はタイムスタンプサーバから始まる。タイムスタンプサーバは、タイムスタンプを行う各アイテムを構成するブロックのハッシュを取得し、そのハッシュを新聞やUsenetポスト[2-5]の様に広く公開する事で機能する。タイムスタンプは、ハッシュ化されるデータがタイムスタンプを行った時点で間違いなく存在していた事を証明する。各タイムスタンプはハッシュ内にその一つ前のタイムスタンプを含み、ブロックチェーンを形成する。つまり、タイムスタンプを行う毎に、一つ前のタイムスタンプを補強するのである。
Proof-of-Work
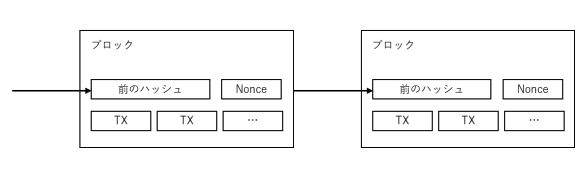
P2Pを基盤とした分散型タイムスタンプサーバを実装するためには、新聞やUsenetの様なものではなく、Adam BackのHashcash[6]と同様のProof-of-Workシステムを使用する必要がある。Proof-of-Workの役割としては、数値がSHA-256等によりハッシュ化された際、最初のnビットが全て0で始まる値を発見する事が挙げられる。要求される平均計算量は、必要な0のビット数に応じて指数関数的に増加する一方、検証については一つのハッシュ関数の計算により可能である。本論文のタイムスタンプネットワークでは、ブロック内のハッシュに対して必要なゼロビットの値が見つかるまで、ブロック内のナンスの値を変化させ、Proof-of-Workを実行する。Proof-of-Workが完了した場合、再計算を伴わずしてブロックを変更する事はできない。あるブロックを変更しようとする場合、そのブロ ックに連鎖する後方のブロックについても、再計算が必要となる。
また、Proof-of-Workは集団の意思決定において、誰が代表かを決定する問題を解決する。多数決方式の様に各IPアドレスに1票ずつを割り当てる方法では、誰かがIPアドレスを大量に確保した時点でシステムを乗っ取ることが可能となる。Proof-of-Workにおける本人確認は原則として1CPU1票である。また、Proof-of-Workの計算量が最も使用されたチェーンが最長チェーンとなり、これが集団の意思決定における代表となる。大多数のCPUパワーが善良なノードによって制御されている場合であれば、そのチェーンは最も速く成長し、競合するチェーンを退ける。過去のある時点のブロックを変更するためには、攻撃者はそのブロックとそれ以降の全てのブロックのProof-of-Workの再計算を行い、善良なノードの計算に追いつき更に上回る必要がある。後述の様に、攻撃者が追いつく確率は、後続ブロックの追加毎に指数関数的に減少する。
年月の経過に伴うハードウェア能力の増加と実行中のノードの関心の変化に伴う影響を考慮し、Proof-of-Workの難易度は、1時間あたりの平均ブロック数を基にした移動平均により定められる。各ブロックがあまりにも速く生成された場合、難易度が増加するのである。
ネットワーク
ネットワークの作動手順は以下の通りである。
1) 新しいトランザクションは全ノードに送信される。
2) 各ノードが新しいトランザクションをあるブロックに取り入れる。
3) 各ノードがそのブロックに対するProof-of-Workを算出する。
4) Proof-of-Workを見つけ次第、ノードはそのブロックを全ノードにブロードキャストする。
5) 各ノードは、そのブロック内の全トランザクションが有効かつ未使用の場合のみ、承認を行う。
6) 各ノードは、承認したブロックのハッシュを直前のハッシュとして使用し、次のブロックの作成を開始することで、ブロックの承認を表明する。
ノードは常に最長チェーンを正しいものと判断し、延長を続ける。2つのノードが異なる2つのブロックを次のブロックとして同時にブロードキャストする場合、ノードによって受信順序が異なる可能性がある。その場合、各ノードは最初の受信分を処理するが、後の受信分も保存してチェーンが長くなった場合に備える。次のProof-of-Workが発見され、どちらかのチェーンが伸びた時に、短い側のチェーンに取り組んでいたノードは長いチェーンに切り替える事となる。
新しいトランザクションのブロードキャストは全ノードに届く必要はない。多数のノードにブロードキャストされる限り、いつかはブロックに組み込まれるのである。また、ブロックのブロードキャストは、メッセージの欠損も想定内である。つまり、ノードがブロックを受信しなかった場合、次のブロックを受信する際にそれを要求し、欠損部分を認識するのである。
インセンティブ
ブロック内の最初のトランザクションは、新しいコインを生成し始める上で特別なものであり、そのコインはブロック作成者のものとなる。これは各ノードがネットワークを支持するインセンティブになると同時に、コインを発行する中央機関が不在の中、最初にコインを発行する方法としても機能する。一定量の新しいコインを安定的に追加していく事は、金鉱労働者が採掘して金の流通量を増加させる事に類似している。本システムにおける採掘は、費やすCPU時間と電力である。
インセンティブは、トランザクション手数料によっても獲得できる。もし、あるトランザクションで受信額が送信額よりも少ない場合、その差額はトランザクション手数料として、そのトランザクションを含むブロック作成者のインセンティブに加算される。コインの流通量が既定値に達すると、インセンティブは完全にトランザクション手数料のみとなり、インフレから完全に解放される。
インセンティブはノードが善意であり続ける動機となり得る。強欲な攻撃者が善意のノードの合計 CPUパワーを上回った場合、善意のノードから自己の支払額を盗んで取り戻すか、新しいコインを作り出すかの２択となる。自己の資産とそれを支えるシステムを損なうよりも、ルールに従って行動し、他の全ノードを合わせたよりも多くの新しいコインを獲得する方が、自己の利益になると考えるだろう。
ディスク・スペースの節約
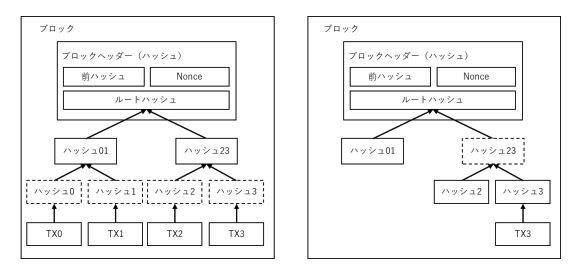
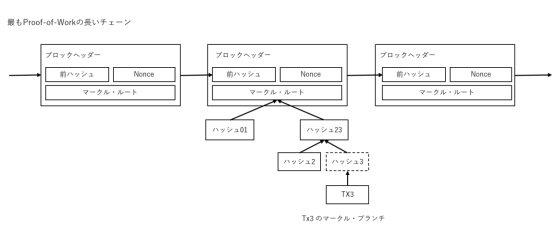
コインの最新のトランザクションが十分な数のブロックに書き込まれると、それ以前のトランザクション記録はディスク・スペース節約のため破棄できる。ブロックのハッシュを壊さずにこの作業を行うため、トランザクションはそのブロックにルートハッシュのみ含み、マークル・ツリー（Merkle Tree[7][2][5]）を用いてハッシュ化される。古いブロックは、ツリーのブランチを除去する事で、スペースを節約できる。こうして、ルートハッシュ以外を保存する必要は無くなる。
トランザクションが無い場合のブロック・ヘッダーの大きさは約80bytesである。仮に10分毎に1つのブロックが作成されると仮定すると、80 bytes × 6 ×24 ×365 = 4.2MB／年となる。2008年の時点で、平均的なパソコンは2GBのRAMで販売されており、ムーアの法則によると1.2GB／年のペースでRAMが増大すると予測されるため、ブロック・ヘッダーをメモリに保存する必要があっても、スペースの問題は無い筈である。
トランザクションの簡易検証
完全にネットワークノードを実行していなくとも、支払いの検証は可能である。つまり、ユーザーは、ネットワークノードに要求する事により得られる、最長のチェーンの各ブロック・ヘッダーのコピーを保存しておくだけで良い。これにより、タイムスタンプが行われたブロックにリンクしているマークル・ブランチを得られるためである。ユーザー自身はトランザクションの確認ができないが、各ブロックの確認により、各ネットワークノードがそのトランザクションを承認済である事が確認でき、後に連鎖するブロックの存在から、ネットワーク全体が承認済である事が確認できる。
このように、善意のノードがネットワークをコントロールする限り、検証も信頼が置けるが、ネットワークが攻撃者に乗っ取られた場合には脆弱となる。各ネットワークノードは自身でトランザクションを検証可能な一方、この簡易なトランザクション検証方法では、攻撃者がネットワークを乗っ取り続ける限り、彼らによって偽造されたトランザクションに騙される事となる。対処方法の1つとしては、各ネットワークノードが不正ブロックを検知した際に発するアラートを受信する設定とし、ユーザー側のソフトウェアに直ちにブロック全体とアラートされたトランザクションをダウンロードさせ、不一致を確認させる事である。支払いを頻繁に受け取るビジネスにおいては、より独立した安全性と迅速な検証のため、独自ノードを運営する方が良いだろう。
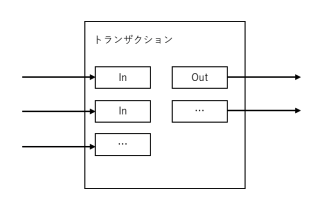
価値の結合および分割
コインを個別に扱う事も可能であるが、トランザクション金額を１セントずつ個別に扱うのは不便だろう。価値の分割や結合を可能にするため、トランザクションには複数のインプットとアウトプットが含まれる。通常、インプットは、価値のより大きな前トランザクションからの1つのものか、小額のものを組み合わせた複数のものに分別される。一方、アウトプットは、支払い目的のものと、もし釣銭があればそれを支払い元に返還するものに分別される。
1つのトランザクションが複数トランザクションに依存し、それらが更に多数のトランザクションに依存するのは問題でない事に留意する必要がある。これは、あるトランザクション履歴から完全に独立したコピーを抽出する必要性はないためである。
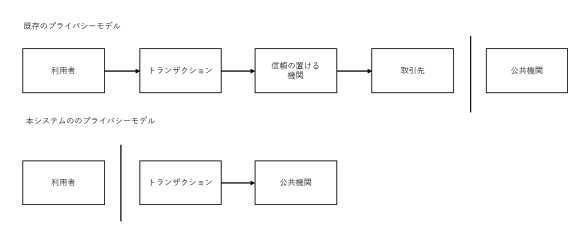
プライバシー
伝統的な銀行モデルでは、情報へのアクセスを関連団体と信頼の置ける第三者機関に限定する事で、一定レベルのプライバシーを実現している。本システムでは、全トランザクションを公開する必要性があるため、上記モデルとは異なるが、情報のフローを他の箇所で分断する事でプライバシーを保守できる。つまり、パブリック・キーを匿名にするのである。誰かが誰かにどれだけのコインを送付したかは公開されるが、そのトランザクション情報は誰にもリンクされていない。これは証券取引で公表されるものと同等の情報レベルであり、個別のトランザクションの時間、数量およびティッカーシンボルは公開されたとしても、そのトランザクションの当事者自体は公開されないのである。
更なる安全策として、同一所有者にリンクする事を防止するため、トランザクションは1回毎に新しいペアのキーを用いても良いだろう。複数インプットの場合、それらが同一の所有者である事が明らかとなるため、リンクを避ける事はできない。また、キーの所有者が明らかとなった場合、その所有者が関わった他のトランザクションも明らかとなるリスクもある。
数学的根拠
攻撃者が善意のチェーンより速いスピードで偽のチェーンを生成しようと試みるシナリオを考察する。仮にそれが成功したとしても、コインを無から生成したり、攻撃者自身が所有した事のないコインを取得したり、と言ったようにシステムを自由に変更できるわけではない。各ノードは無効なトランザクションやそのトランザクションを含んだブロックを拒絶するのである。攻撃者は自身のトランザクション記録を書き換える事で、最近の支払金額を取り返そうとする事のみが可能である。善意のチェーンと攻撃者のチェーンの競争は2項ランダムウォークで説明が可能である。成功イベントは善意のチェーンが1ブロック延長して差が1つ広まる事、失敗イベントは攻撃者のチェーンが1ブロック延長して差が1つ縮まる事である。攻撃者が遅れを取り戻す確率はギャンブラーの破産問題に類似する。無限の資金を持つギャンブラーが赤字からスタートして損益分岐点を目指して無数の賭けを行うと仮定すると、ギャンブラーが損益分岐点に到達する確率、または攻撃者が善意のチェーンに追いつく確率は以下の様に計算可能である。
P = 善意のノードが次のブロックを見つける確率
q = 攻撃者が次のブロックを見つける確率
qz= 攻撃者がzブロックの遅れから追いつく確率
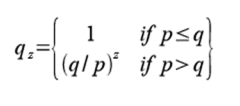p＞qという仮定を前提とすると、追いつく必要があるブロック数の増加に伴い、攻撃者が追いつく確率は指数関数的に下がっていく。この分の悪い確率の基では、初期段階で余程の幸運に恵まれない限り、彼が追いつく確率は後れを取るに連れて極めて小さくなる。次に、新しいトランザクションの受け手が、送り手がトランザクション内容を変更できないと確信できるまでに、どれだけの時間待つ必要があるかを考察する。送り手が攻撃者で、受け手に支払いを済ませたと暫くの間信じ込ませた後、自分に払い戻そうとしていると仮定する。その場合、受け手はアラートを受信するが、攻撃者はその時点で既に手遅れである事を期待する。
受け手はパブリック・キーを作成し、電子署名する直前にそれを送り手に送付する。これにより、送り手が前もって偽のチェーンを用意し、パブリック・キーが送付された瞬間に偽のトランザクションを行う事を防止できる。トランザクションが送信されると直ちに、不正な送り手（攻撃者）は密かに別のトランザクションを含んだパラレル・チェーンの生成に着手する。受け手は自分のトランザクションがブロックに追加され、z個のブロックがその後にリンクされるまで待機する。受け手には攻撃者の正確な進捗は分からないが、正当なブロックが平均的な時間で作成されたと仮定すると、攻撃者の進捗は以下のポアソン分布の期待値から算出可能である。
攻撃者がこの時点で追いつく事が可能な確率を算出するためには、彼が行った各仕事量あたりのポアソン分布密度を、その時点で追いつく事ができた確率に掛ければ良い。
分布の無限テールの加算がされないよう式変形すると、以下の通りとなる。
上記の式をCコードに変換すると、以下の通りとなる。
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
{
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
}
return sum;
}
以下の通り、攻撃者が追いつく確率はzの増加と共に、指数関数的に減少することがわかるだろう。 q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
P（攻撃者が追いつく確率）を0.1％より少なくする場合のqとzの解の種類は、以下の通りとなる。P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
結論
本論文では、トラストレスな電子取引のシステムを提案した。電子署名により生成される従来通りのフレームワークに基づくコインは、所有権を強くコントロールできるが、二重支払いの防止策無しには不完全である。その解決策として、善意のノードがCPUパワーの過半数をコントロールする限り、Proof-of-Workにより記録した公開取引履歴を攻撃者が改ざんする事が、計算上加速度的に不可能となっていくP2Pネットワークを提案した。ネットワーク自体はシンプルであり堅固なものである。また、各ノードは同時に動作するものの協調性は低い。メッセージは特定の場所に届けられず、ベストエフォート方式で送信すれば良いため、各ノードが特定される必要性はない。各ノードは自由にネットワークに離脱・再接続でき、離脱していた間のProof-of-Workチェーンをその間の取引証明として承認する。各ノードはCPUパワーを用い、受信したブロックが有効だと判断した場合にはそのブロックを延長する事で承認を表明し、無効なブロックだと判断した場合にはその処理を拒否する事で拒絶を表明する。ルールやインセンティブは全てこの合意メカニズムに従って実行される。
参考文献
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,” In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, “Hashcash-a denial of service counter-measure,” http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “An introduction to probability theory and its applications,” 1957